ЕГЭ Физика 2018 — Все ли мы знаем об отражении света?

Если световой луч опускается на рубеж области 2-ух сред, совершается отражение света: луч меняет течение собственного хода и возвратится в начальную среду. На рис. 1 представлены падающий луч AO, отражённый луч OB, а также перпендикуляр OC, проведённый к отражающей поверхности KL в точке падения O.

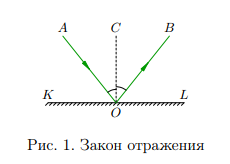
Угол AOC именуется углом падения. Обратите внимание и помните: угол падения отсчитывается от перпендикуляра к отражающей поверхности, а никак не от самой поверхности! Точно таким образом угол отражения — это угол BOC, образованный отражённым лучом и перпендикуляром к поверхности.

Закон отражения

1) Падающий луч, отражённый луч и перпендикуляр к отражающей поверхности, проведённый в точке падения, лежат в одной плоскости.

2) Угол отражения равен углу падения.

Таким образом, ∠AOC = ∠BOC, что и показано на рис. 1.

Закон отражения обладает одим простым, однако весьма существенным геометрическим следствием. Давайте посмотрим на рис. 2. Пусть из точки A идет световой луч. Выстроим точку A0 , симметричную точке A относительно отражающей поверхности KL.

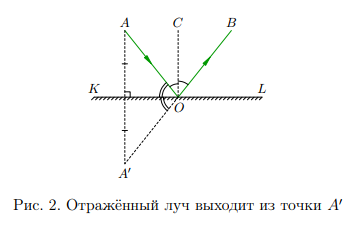
Из симметрии точек A и A0ясно, что ∠AOK = ∠A0OK. Кроме того, ∠AOK + ∠AOC = 90◦ . Поэтому ∠A0OB = 2(∠AOK + ∠AOC) = 180◦ , и, следовательно, точки A0 , O и B лежат на одной прямой! Отражённый луч OB как бы выходит из точки A0 , симметричной точке A относительно отражающей поверхности. Этот факт нам понадобится в самом недалеком времени.

Закон отражения представляет ход отдельных световых лучей — узких пучков света. Однако в многочисленных случаях пучок является довольно широким, то есть состоит из множества параллельных лучей. Картина отражения широкого пучка света станет зависеть от свойств отражающей поверхности.

Если поверхность является неровной, то после отражения параллельность лучей нарушится. В качестве примера на рис. 3 представлено отражение с волнообразной поверхности. Отражённые лучи, как видно, проходят в самых различных направлениях.

Однако что означает «неровная» поверхность? Какие поверхности считаются «ровными»? Ответ такой: поверхность является неровной, в случае если размеры ее неровностей не менее длины световых волн. Таким образом, на рис. 3 типичный размер неровностей на несколько порядков превышает значение длин волн зримого света.

Поверхность с микроскопическими неровностями, пропорциональными с длинами волн зримого света, именуется матовой. В следствии отражения параллельного пучка от матовой поверхности выходит рассеянный свет — лучи этого света проходят в различных направлениях. Само отражение от матовой поверхности по этой причине рассеянным либо диффузным.

Если же размер неровностей поверхности менее длины световой волны, то такая поверхность именуется зеркальной. При отражении от зеркальной поверхности параллельность пучка сохраняется: кроме того, отражённые лучи идут параллельно (рис. 4).

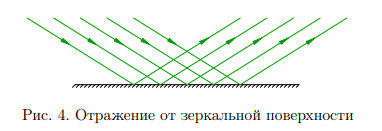
Приблизительно зеркальной считается гладкая плоскость воды, стекла либо отполированного металла. Отражение от зеркальной поверхности именуется соответственно зеркальным. Нас будет интересовать простой, однако значительный индивидуальный случай зеркального отражения — отражение в плоском зеркале.

Плоское зеркало — это доля плоскости, зеркально отражающая свет. Плоское зеркало — обыкновенная вещь; подобных зеркал несколько в вашем жилье. Но сейчас мы сможем понять, по какой причине, смотрясь в зеркало, вы видите в нём отражение себя и пребывающих вблизи с вами объектов.

Точечный источник света S на рис. 5 испускает лучи в различных направлениях; давайте возьмём 2 близких луча, падающих на плоское зеркало. Мы уже знаем, что отражённые лучи направятся таким образом, будто бы они исходят из точки S 0 , симметричной точке S относительно плоскости зеркала.

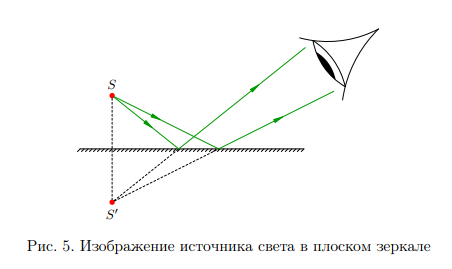
Наиболее увлекательное наступает, когда расходящиеся отражённые лучи попадают к нам в глаза. Отличительная черта нашего сознания заключается в том, что мозг достраивает расходящийся пучок, продолжая его за зеркало вплоть до пересечения в точке S’. Нам может показаться на первый взгляд, что отражённые лучи исходят из точки S’ — мы видим там светящуюся точку!

Эта точка служит изображением источника света S. Безусловно, в действительности ничего за зеркалом не светится, никакая энергия там никак не сконцентрирована — это иллюзия, обман зрения, порождение нашего сознания. По этой причине точка S называется мнимым изображением источника S. В точке S пересекаются не сами световые лучи, а их мысленные продолжения «в зазеркалье».

Ясно, то что изображение S’ станет существовать вне зависимости от размеров зеркала и от того, пребывает ли источник непосредственно над зеркалом либо нет (злак. 6). Важно только, чтобы отражённые от зеркала лучи попадали в глаз — а уж глаза сами образует изображение источника.

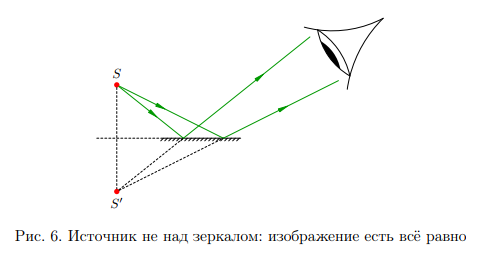
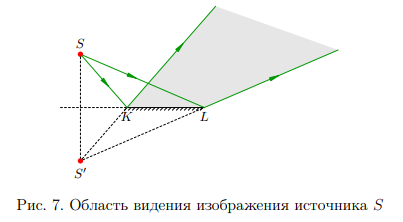
От местоположения источника и размеров зеркала находится в зависимости область видения — пространственая область, из которой видно изображение источника. Область видения задаётся краями K и 3 L зеркала KL. Построение области видения изображения S ясно из рис. 7; искомая область видения выделена сероватым фоном.

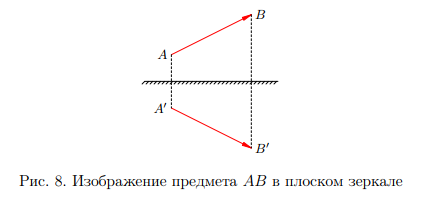
Как построить изображение произвольного объекта в плоском зеркале? Для этого достаточно отыскать изображение каждой точки данного объекта. Однако мы знаем, что изображение точки симметрично самой точке относительно зеркала. Таким образом, изображение предмета в плоском зеркале симметрично предмету относительно плоскости зеркала (рис. 8).

Расположение объекта относительно зеркала и размеры самого зеркала никак не оказывают влияния на изображение (рис. 9).